Hypothesis formulation
Based on research review, it appears that while more women have joined the labor force thanks to urbanization, they have encountered several cultural and social obstacles that have negatively impacted their employment rates. It would be interesting to study the correlation between urbanization and the female employment rate in the Gapminder dataset. Hypothesis: Higher urbanization rates lead to lower female employment rates.
Testing Statistical Interaction or Moderation In The Context of ANOVA
The goal in this exercise is to determine if the explanatory variable (urbanization rate) is associated with the response variable (female employ rate), for each level of a third categorical variable, in this case 'income per person'. The income levels were grouped by dividing the 'income per person' values into 6 levels. The urbanization rate values were were grouped into 6 levels in a previous assignment.
/** Grouping income per person **/
DATA NEW; /** Creates new variable that will be the SAS output data set**/
SET work.newdata; /** Reads observations from the SAS dataset**/
KEEP femaleemployrate employrate urbanrate incomeperperson
FemaleEmploymentRateGroup EmploymentRateGroup
UrbanizationRateGroup IncomePerPersonGroup;
if (incomeperperson ^= . & incomeperperson <= 800) then
IncomePerPersonGroup = "1";
if (incomeperperson > 800 & incomeperperson <= 2000) then
IncomePerPersonGroup = "2";
if (incomeperperson > 2000 & incomeperperson <= 8000) then
IncomePerPersonGroup = "3";
if (incomeperperson > 8000 & incomeperperson <= 18000) then
IncomePerPersonGroup = "4";
if (incomeperperson > 18000 & incomeperperson <= 24000) then
IncomePerPersonGroup = "5";
if (incomeperperson > 24000) then
IncomePerPersonGroup ="6";
RUN;
The ANOVA procedure was then generated to test for moderation for each level of IncomePerPersonGroup:
/** TESTING MODERATION IN THE CONTEXT OF ANOVA **/
PROC SORT DATA=NEW;
BY IncomePerPersonGroup;
RUN;
PROC ANOVA DATA=NEW;
CLASS UrbanizationRateGroup;
MODEL femaleemployrate = UrbanizationRateGroup;
MEANS UrbanizationRateGroup;
BY IncomePerPersonGroup;
RUN;
Results:
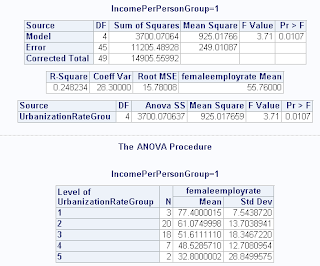
The results show an inverse association between the female employ rate and urbanization rate in the first / lowest income level, where the income per person is $800 or lower. At this income level, the P-value is statistically significant (0.0107) and has the highest F value among the 6 levels. The means table shows that urbanization rate group 1 (lowest level) has the highest mean value of female employ rate (77.4) compared to levels 2 - 6.
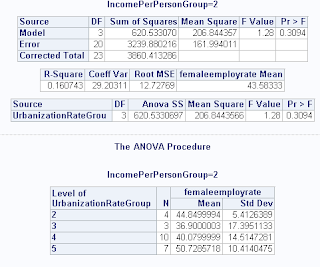
The higher Income levels 2 - 6 have P-values higher than 0.05 and are therefore not statistically significant.
Testing Statistical Interaction or Moderation In The Context of CHI SQUARE
PROC GCHART;
VBAR UrbanizationRateGroup / DISCRETE TYPE=MEAN SUMVAR=femaleemployrate;
RUN;
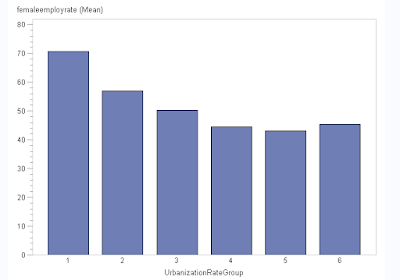
A bar chart reveals an inverse association between female employ rate and the urban rate.
/** TESTING MODERATION IN THE CONTEXT OF CHI SQUARE TEST OF INDEPENDENCE **/
PROC SORT DATA=NEW;
BY IncomePerPersonGroup;
RUN;
PROC FREQ DATA=NEW;
TABLES FemaleEmploymentRateGroup * UrbanizationRateGroup / CHISQ;
BY IncomePerPersonGroup;
RUN;
Results:
The results show an inverse association between the female employ rate and urbanization rate in the first and third income levels, where the income per person are $800 or lower, and between $2,000-$8,000. At these income levels, the P-values are statistically significant (0.0015 for income level 1 and 0.0087 for income level 3) and have the highest Chi Square values of 44.1 for income level 1 and 26.6 for income level 3. Income levels 2, 4, 5 and 6 have P-values higher than 0.05 and are therefore not statistically significant.
Testing Statistical Interaction or Moderation In The Context of the Pearson Correlation Coefficient
/** TESTING MODERATION IN THE CONTEXT OF CORRELATION **/
PROC SORT DATA=NEW;
BY IncomePerPersonGroup;
RUN;
PROC CORR DATA=NEW;
VAR urbanrate femaleemployrate;
BY IncomePerPersonGroup;
RUN;
Results:
The results show an inverse association between the female employ rate and urbanization rate in the first income level, where the income per person is $800 or lower. At this income level, the P-value is statistically significant (0.0006) with a correlation co-efficient of -.46785. Income levels 2,3, 4, 5 and 6 have P-values higher than 0.05 and are therefore not statistically significant.